Big-O // KONPIG BLOG

Big-O 표기법이란 알고리즘의 효율성을 나타내는 지표 혹은 언어를 말한다.

보통 알고리즘의 시간복잡도와 공간복잡도를 나타낼 때 사용한다.

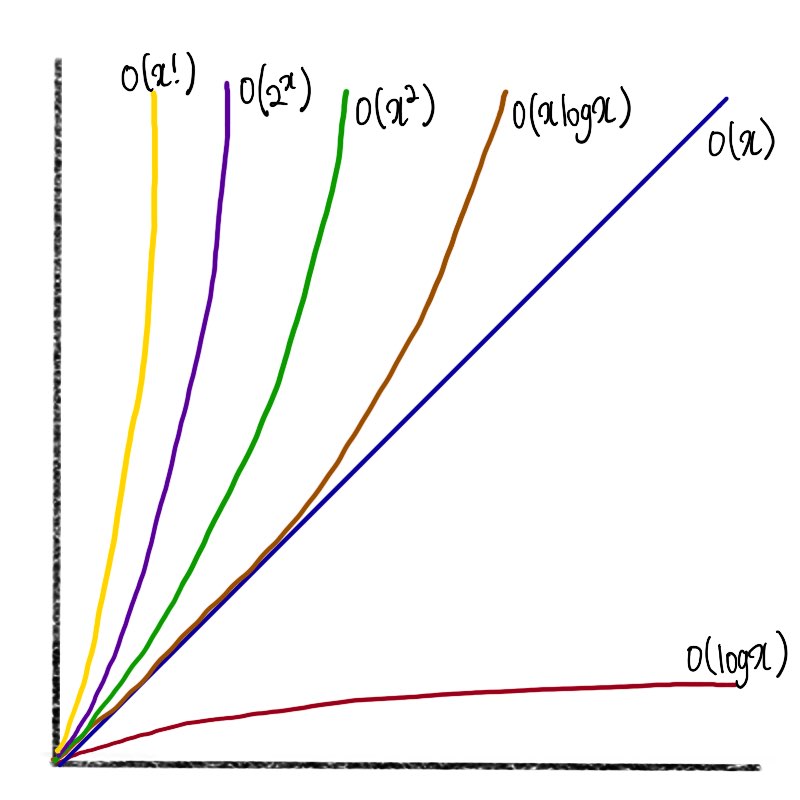
비교 그래프

자주 사용하는 Big-O 표기법을 효율성이 좋은 것 부터 나열해보자면 아래와 같다.

O(1) < O(logN) < O(N) < O(NlogN) < O(N^2) < O(2N) < O(N!) < O(N^N)

graph

(아이패드 첫 사용 기념으로 애플펜슬로 그려봤는데 발로 그린 게 더 낫겠다.)

하나의 알고리즘에서 최선, 최악, 평균 시간을 구할 수 있다.

퀵정렬을 예로 들어 간단히 설명하자면, N을 배열의 크기라고 가정했을 때

최선 : 모든 원소들이 같은 값일 때 시간복잡도 -> O(N)
최악 : 배열의 가장 큰 원소가 계속 축이 될 때 시간복잡도 -> O(N^2)

- 배열을 절반으로 나누지 못하고 계속 한 개씩만 줄어든 배열로 리턴
평균 : 배열을 절반으로 나누어 정렬할 때 시간복잡도 -> O(NlogN)

퀵정렬이란?

축이 되는 원소를 무작위로 하나 정하여 축보다 작은 원소들은 앞으로, 큰 원소들은 뒤로 놓이도록 Swap을 반복하여 정렬하는 방법

Big-O는 효율성의 비율을 나타내는 개념으로 입력값이 충분히 크다고 가정한다.

따라서 사소한 부분(계산에 큰 영향을 미치지 않는)은 무시할 수 있다.

실행순서에 따라 수행시간 계산 방식이 달라진다.

O(A + B) : A를 끝마친 후에 B 수행

for(int a : arrA){
    print(a);
}
  
for(int b : arrB){
    print(b);
}

O(A * B) : A가 할 때마다 B 수행

for(int a : arrA){
  for(int b : arrB){
      print(a + ", " + b);
  }
}

O(logN) : 이진탐색, 균형 이진탐색트리 사용 시 확인할 수 있다.

탐색 과정
1. 원소 x와 배열의 중간값 m을 비교
2. x==m 일 때 반환 또는 x<m 일 때 배열의 왼쪽 부분 재탐색
처음 N개에서 한 단계씩 거치면서 탐색할 원소의 개수가 N/2, N/4, … 로 줄어든다.

따라서 총 수행시간은 N을 절반씩 나누는 과정에서 몇 단계만에 1이 되는지에 따라 결정된다.
N이 16일 때 16에서 1로 감소하는 순서를 뒤집어서 1에서 16으로 증가하는 순서로 생각해보면,

숫자 1에 2를 4번 곱해야 N이 된다. 즉, 2^k = N을 만족하는 k를 구할 때 사용되는 것이 log이다.

이진탐색이란? N개의 정렬된 원소가 들어있는 배열에서 원소 x를 찾을 때 사용하는 방법이다.

깊이가 N인 트리의 전체 노드의 개수 = 2의 승수의 합 = ( 2^(N+1) - 1 )

게일 라크만 맥도웰, 코딩 인터뷰 완전 분석, 인사이트, 2017